Java 优先队列 PriorityQueue
引言
在Java集合框架中,优先队列PriorityQueue实现了接口Queue,但是PriorityQueue并没有保留Queue先进先出(FIFO)的特点,而是采用按优先级顺序的访问元素。
下面看一个简单的PriorityQueue和Queue的对比示意图:
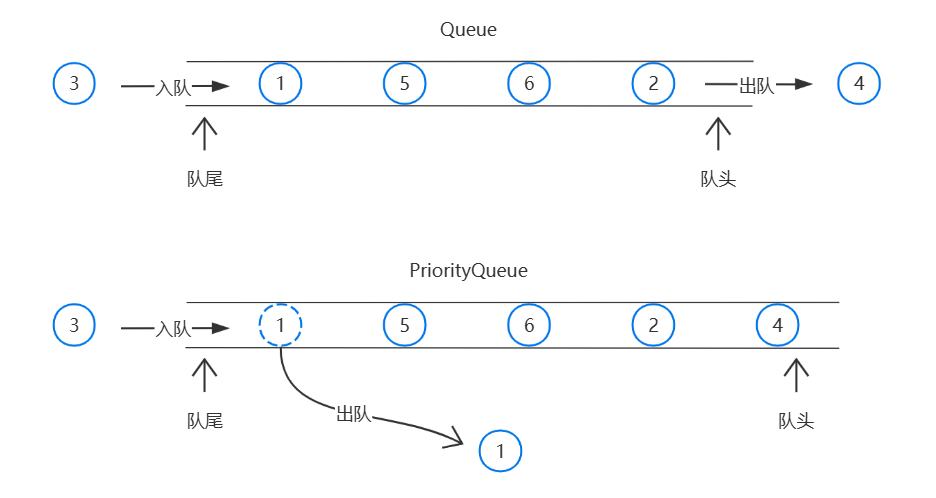
查看示意图可以发现PriorityQueue并没有像普通队列一样先入先出,每次都是当前队列中最小的元素出队。优先队列的元素是按排序顺序检索的,默认是以升序进行检索的,但是优先队列内的元素可能并没有排序。
初始化PriorityQueue
在创建PriorityQueue的时候,JDK提供了多种初始化方法供我们适配不同的场景进行使用。其中包含初始的无参构造函数、比较器、集合等方式。下面只会使用常用的无参和比较器进行展示,其他的难度并不大,如果有兴趣可以自行探索。
普通初始化
先看下源码中无参构造方法的注释
Creates a PriorityQueue with the default initial capacity (11) that orders its elements according to their natural ordering.
创建一个默认初始容量为11的并且会根据自然排序对元素进行检索
PriorityQueue<Integer> numbers = new PriorityQueue<>();比较器初始化
Creates a PriorityQueue with the default initial capacity and whose elements are ordered according to the specified comparator.
Params: comparator – the comparator that will be used to order this priority queue. If null, the natural ordering of the elements will be used.
创建一个默认初始容量的优先级队列,且容器中的元素根据指定的比较器的规则进行排序,如果比较器为null,则使用元素的自然顺序
public class Main {
public static void main(String[] args) {
PriorityQueue<Integer> numbers = new PriorityQueue<>(new myComparator());
}
}
class myComparator implements Comparator<Integer> {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
}使用比较器创建的方式并非只有一种,还可以是
static Comparator<Integer> com = new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
};
public class Main {
public static void main(String[] args) {
PriorityQueue<Integer> numbers = new PriorityQueue<>(com);
}
}或者
PriorityQueue<Integer> numbers = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
});因为当前比较器的逻辑比较简单,也可以直接写成Lambda表达式形式,在Idea中也会有提示
PriorityQueue<Integer> numbers = new PriorityQueue<>((o1, o2) -> o2 - o1);PriorityQueue方法
| 方法名 | 描述 |
|---|---|
boolean add(E e) | 将指定元素插入此优先级队列。 |
boolean offer(E e) | 将指定元素插入此优先级队列。 |
E peek() | 检索但不删除此队列的头部,如果此队列为空,则返回null。 |
boolean remove(Object o) | 如果该队列包含一个或多个此类元素,则删除元素e的单个实例 |
boolean contains(Object o) | 如果此队列包含指定元素,则返回true。 |
int size() | 返回此集合中的元素数。 |
void clear() | 从此优先级队列中删除所有元素。此调用返回后队列将为空。 |
E poll() | 检索并删除此队列的头部,如果此队列为空,则返回null。 |
插入PriorityQueue元素
PriorityQueue中提供了两种插入的方法add(E e)和offer(E e),这两个方法在PriorityQueue中并无区别。看一下add(E e)的源码就明白了
public class PriorityQueue<E> extends AbstractQueue<E>
implements java.io.Serializable {
//...................
public boolean add(E e) {
return offer(e);
}
public boolean offer(E e) {
if (e == null)
throw new NullPointerException();
modCount++;
int i = size;
if (i >= queue.length)
grow(i + 1);
siftUp(i, e);
size = i + 1;
return true;
}
//...................
}public class Main {
public static void main(String[] args) {
PriorityQueue<Integer> numbers = new PriorityQueue<>(3);
numbers.add(4);
numbers.add(2);
numbers.add(6);
numbers.add(5);
System.out.println("更新前的PriorityQueue: " +numbers);
numbers.offer(3);
System.out.println("更新后的PriorityQueue: " + numbers);
}
}输出结果
更新前的PriorityQueue: [2, 4, 6, 5]
更新后的PriorityQueue: [2, 3, 6, 5, 4]删除PriorityQueue元素
PriorityQueue提供了多个删除元素的方方法。
poll()
poll()方法的作用是获取并删除队首元素。
public class Main {
public static void main(String[] args) {
PriorityQueue<Integer> numbers = new PriorityQueue<>();
numbers.add(4);
numbers.add(2);
numbers.add(6);
numbers.add(5);
System.out.println("更新前的PriorityQueue: " + numbers);
numbers.poll();
System.out.println("更新后的PriorityQueue: " + numbers);
}
}输出结果
更新前的PriorityQueue: [2, 4, 6, 5]
更新后的PriorityQueue: [4, 5, 6]remove(Object o)
remove(Object o)方法的作用如果在不指定参数的情况下,其功能与poll()的功能完全相同。如果指定参数则是删除该队列中指定元素的单个实例。
public class Main {
public static void main(String[] args) {
PriorityQueue<Integer> numbers = new PriorityQueue<>(3);
numbers.add(4);
numbers.add(2);
numbers.add(6);
numbers.add(5);
numbers.add(5);
System.out.println("更新前的PriorityQueue: " + numbers);
numbers.remove();
System.out.println("更新后的PriorityQueue: " + numbers);
numbers.remove(5);
System.out.println("更新后的PriorityQueue: " + numbers);
}
}输出结果
更新前的PriorityQueue: [2, 4, 6, 5, 5]
更新后的PriorityQueue: [4, 5, 6, 5]
更新后的PriorityQueue: [4, 5, 6]clear()
clear()方法的作用是清空PriorityQueue中的所有元素。
public class Main {
public static void main(String[] args) {
PriorityQueue<Integer> numbers = new PriorityQueue<>(3);
numbers.add(4);
numbers.add(2);
numbers.add(6);
numbers.add(5);
System.out.println("更新前的PriorityQueue: " + numbers);
numbers.clear();
System.out.println("更新后的PriorityQueue: " + numbers);
}
}输出结果
更新前的PriorityQueue: [2, 4, 6, 5]
更新后的PriorityQueue: []访问PriorityQueue元素
要从优先级队列中访问元素,可以使用peek()方法,它的作用是检索该队列的头部,但是不删除,如果队列为空,则返回NULL
public class Main {
public static void main(String[] args) {
PriorityQueue<Integer> numbers = new PriorityQueue<>();
numbers.add(4);
numbers.add(2);
numbers.add(6);
numbers.add(5);
System.out.println("PriorityQueue: " + numbers);
Integer peek = numbers.peek();
System.out.println("调用peek()方法结果: " + peek);
}
}输出结果
PriorityQueue: [2, 4, 6, 5]
调用peek()方法结果: 2遍历PriorityQueue
如果需要遍历优先级队列中的所有元素,我们有多种方式可以选择,例如
使用for-each循环
public class Main {
public static void main(String[] args) {
PriorityQueue<Integer> numbers = new PriorityQueue<>();
numbers.add(4);
numbers.add(2);
numbers.add(6);
numbers.add(5);
System.out.println("PriorityQueue: " + numbers);
for (Integer number : numbers) {
System.out.println(number);
}
}
}使用iterator()方法
public class Main {
public static void main(String[] args) {
PriorityQueue<Integer> numbers = new PriorityQueue<>();
numbers.add(4);
numbers.add(2);
numbers.add(6);
numbers.add(5);
System.out.println(numbers);
Iterator<Integer> iterator = numbers.iterator();
while (iterator.hasNext()) {
System.out.println(iterator.next());
}
}
}使用forEach()方法
public class Main {
public static void main(String[] args) {
PriorityQueue<Integer> numbers = new PriorityQueue<>();
numbers.add(4);
numbers.add(2);
numbers.add(6);
numbers.add(5);
System.out.println("PriorityQueue: " + numbers);
numbers.forEach(System.out::println);
}
}输出结果
PriorityQueue: [2, 4, 6, 5]
2
4
6
5小结
PriorityQueue是基于二叉堆实现的,底层存储结构为Object[],PriorityQueue是一个高效灵活的优先级队列,使用PriorityQueue能够更高效的解决问题,例如求第K大的数,想要熟练使用PriorityQueue,还是需要动手实践,下面推荐练习题作为参考练习。
以上是力扣中关于PriorityQueue的较为简单的题目,如果有兴趣可以挑战更加复杂的当然是最好的。