线性表

李木子约 2363 字大约 8 分钟

作者寄语：

线性表是数据结构中最基本、最简单、也是最常用的一种数据结构。顺序表、链表、栈、队列都是基于线性表的数据结构，包括串，也是一种特殊的线性表。

线性表

定义

线性表(List) 就是包含零个或多个元素的有限序列，中元素是有顺序的，若元素存在多个，则第一个元素无前驱，最后一个元素无后继，其他每个元素都有且只有一个直接前驱和直接后继，线性表中的个数n(n≥0)定义为线性表的长度，当n=0时，称线性表为空表。

抽象数据类型

线性表的抽象数据类型定义了线性表逻辑特性和操作，并不设计具体的实现细节。对于不同的应用，线性表的基本操作是不相同的，并不完全按照抽象数据类型来定义。

ADT List {
    数据对象：
        D = { a_i | a_i ∈ ElemType, i = 1, 2, ..., n, n ≥ 0 }
    数据关系：
        R = { <a_i, a_{i+1}> | a_i, a_{i+1} ∈ D, i = 1, 2, ..., n-1 }
    基本操作：
        InitList(&L)：初始化线性表。
        DestroyList(&L)：销毁线性表。
        ListEmpty(L)：判断线性表是否为空。
        ListLength(L)：返回线性表的长度。
        GetElem(L, i, &e)：获取第 i 个元素。
        LocateElem(L, e)：查找元素 e 的位置。
        ListInsert(&L, i, e)：在第 i 个位置插入元素 e。
        ListDelete(&L, i, &e)：删除第 i 个元素。
        TraverseList(L)：遍历线性表。
        ClearList(&L)：清空线性表。
        PriorElem(L, cur_e, &pre_e)：获取 cur_e 的前驱。
        NextElem(L, cur_e, &next_e)：获取 cur_e 的后继。
}

顺序存储结构

顺序存储结构是线性表中的两种物理结构中的一种。指的是一段地址连续的存储单元，依次存储线性表的数据元素。也就是说核心特点是逻辑上相邻的元素在物理上也相邻。

很多语言中其实是通过一维数组来实现顺序存储的，数组和顺序表在概念上具有一定的相似性，但是两者并不完全相同。数组是一种数据结构，而顺序表是线性表的一种实现方式。

还可以从另一方面分辨两者。数组的长度在创建完成后一般是不变的。而线性表的长度指的是表中数据元素的个数。

优点：

不需要为表示表中元素的逻辑关系而增加额外的存储空间。
可以快速的存取表中的任一元素。

缺点

插入和删除操作需要移动大量元素。插入和删除的事件复杂度为O(n)，而读取仅需O(1)。
当线性表变化较大是，难以确定存储空间的容量。
造成存储空间的碎片。

链式存储结构

链式存储结构不要求逻辑上相邻的元素在物理位置上也相邻因此它没有顺序存储结构的缺点，同时也失去了顺序表可随机存取的优点。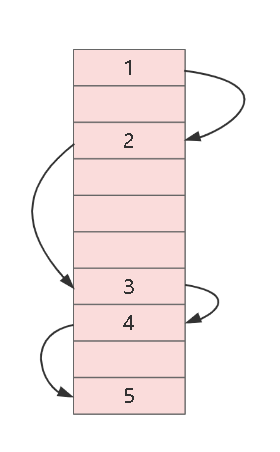

链式存储结构的特点是用一组任意的存储单元存储线性表的数据元素，这组存储单元可以是连续的，也可以是不连续的。也就是说链表可以见缝插针式的存储。

因此为了表示每个数据元素a_i与其直接后继元素a_i+1的逻辑关系，a_i不仅存储自己的信息，还需要额外的空间存储一个指示其直接后继的信息（即直接后继的存储位置）。

存储自己信息的位置称为数据域，存储直接后继位置的位置称为指针域。指针域中的信息称为指针或链。数据与和指针域组成数据元素a_i的存储映像，称为结点。

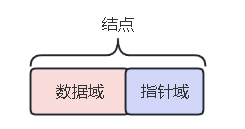
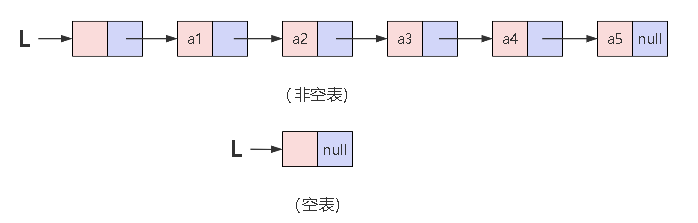
n个结点链接成一个链表就是线性表的链式存储结构。链表中的每个结点只包含一个指针域，也可称为单链表或线性链表。整个链表的存取都必须要从头指针开始进行。头指针指示链表中第一个结点的存储位置。同时，由于最后一个数据元素没有直接后继，线性表中的最后一个结点的指针为NULL

有时，为了方便对链表进行操作，会在单链表的第一个结点之前附设一个头结点，头结点的数据域可以不存储任何信息，也可以存储如线性表长度等类的附加信息。头结点的指针域存储指向第一个结点的指针。若线性表为空表，头结点的指针域指向NULL。

链式存储结构和顺序存储结构的优缺点

存储分配方式： 顺序存储结构用一组连续的存储单元依次存储线性表中的数据元素；链式存储结构用一组任意单元存储线性表中的数据元素。
时间性能： 顺序存储查找性能为O(1)，插入和删除的时间复杂度为O(n)；单链表的查找时间复杂度为O(n)，插入和删除的时间复杂度为O(1)。
空间性能： 顺序存储结构需要预分配存储空间，空间大小难以把控。链式存储结构不需要分配存储空间，只要有就可以分配，元素个数也不受限制。
应用场景： 若线性表需要频繁查找，很少进行插入和删除操作，宜采用顺序存储结构；当线性表中元素个数变化较大或者不确定的时候，宜用单链表结构。

栈

抽象数据类型栈的定义

栈（stack）是限定仅在表尾进行插入或删除操作的线性表。允许插入元素的一端称为栈顶（top），另一端称为栈底（bottom），不含元素的空表称为空栈。栈又称为后进先出（Last In First Out）的线性表，简称LIFO结构。栈的插入操作被称为入栈，删除操作被称为出栈。

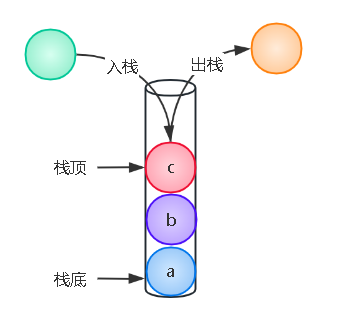
栈的抽象数据类型

栈也是一种线性表，理论上栈具备线性表的所有特性。但是栈的插入和删除操作只能在栈顶进行操作。

ADT Stack {
    数据：
        元素集合：{element1, element2, ..., elementN}
        栈顶指针：top

    操作：
        initStack(): 初始化栈
        push(element): 将元素 element 入栈
        pop(): 移除并返回栈顶元素
        peek(): 返回栈顶元素但不移除
        isEmpty(): 判断栈是否为空
        isFull(): 判断栈是否已满（可选）
        size(): 返回栈的大小
}

队列

抽象数据类型队列的定义

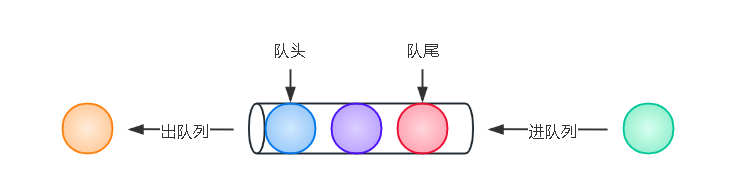
和栈相反，队列（queue）是一种先进先出（first in first out）FIFO的线性表。它只允许在表的一端进行插入，称为队尾；另一端删除元素，称为队头。

队列的抽象数据类型

同样是线性表，插入数据只能在队尾进行操作，删除操作只能在队头进行操作。

ADT Queue {
    数据：
        元素集合：{element1, element2, ..., elementN}
        队头指针：front
        队尾指针：rear

    操作：
        initQueue(): 初始化队列
        enqueue(element): 将元素 element 入队
        dequeue(): 移除并返回队头元素
        peek(): 返回队头元素但不移除
        isEmpty(): 判断队列是否为空
        isFull(): 判断队列是否已满（可选）
        size(): 返回队列的大小
}

ADT String {
    数据：
        字符集合：{char1, char2, ..., charN}
        长度：length

    操作：
        initString(): 初始化串
        assign(source): 赋值
        length(): 获取长度
        isEmpty(): 判断是否为空
        concat(str): 连接
        substring(start, length): 获取子串
        indexOf(subStr): 查找子串
        insert(pos, str): 插入
        delete(start, length): 删除
        replace(oldStr, newStr): 替换
}

线性表

线性表

定义